Economical Passive Activation Solves Bin Hang-ups
Contents
Vibration: A Two-Edged Sword
Conserving Potential Energy
Vertical Bins Walls
Conical Hoppers
Hopper and bin hang-ups are often approached by brute force, for example sledgehammers. This is evident by the severe outbreak of "hopper rash" (hammered pock marks on hoppers and chutes). Often this develops into a fully malletized hopper where the shape has been altered by such severe hammering that it is no longer recognized as the original cone or pyramid shape.
Solving these hopper maladies usually involves vibration, air lances, shakers, air cannons, vibrated (activated) hop-pers, or just plain cussing. The results are less than pleasing. Vibrators and shakers placed on ordinary hoppers often split welds and create ear-splitting noise. Air lances and can-nons create sudden collapses that fluidize powders, making even the slightest crack a no-zzle for fluidized solids. The severe impact of falling solids shaken loose by the vibrators and air cannons often re-compacts the solids worse than before. In extreme cases, the im-pact breaks welds and tears hoppers from their upper vertical bin sections.
Vibration: A Two-Edged Sword
Vibrated (activated) hoppers, suspended to allow the entire hopper to vibrate on hanging supports, seldom give uniform flow across their entire top diameter. This leaves one-half to three-quarters of the material above the bin activator inactive. If the level is maintained within the bin, these inactive regions may harden into solid blocks that either remain as an integral part of the structure or dislodge to block the outlet or annular region around the inside baf-fle of the activated hopper.
When a full bin (the upper vertical section) or hopper (lower converging section) is vibrated, the solids contact pressure increases, the bulk solid compacts and becomes stronger. This in-creased strength makes solids flow less likely. If the vibration increases severely (often severe enough to break hopper welds), its sphere of influence may reach an unconfined surface of the solid such as an unsupported arch or rathole stress-free surface (see Fig. 1). Vibration then increases at the stress-free sur-face and may overcome the strength created by the vibration in the first place. This action initiates flow. If the vibration is left on after flow starts, the cycle of compaction and failure may be repeated. The resulting intermittent flow to a downstream process may be disastrous. When vibration is applied to a springy material like wood chips, sawdust, chopped fiberglass, metal turnings or other springy-type solids, vibration almost always has a negative effect.
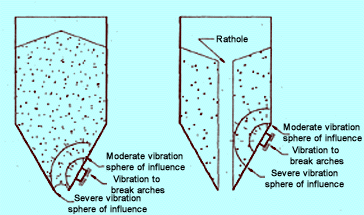
Figure 1: Vibration to break arches and ratholes
Unless vibration is applied at the solid's stress-free surface, over-compaction results and often requires more and heavier bin vibration to in-itiate flow. Hence, there is a self-perpetuating, destructive cycle. If the vibration sphere of in-fluence does not include a stress-free surface of an arch or rathole, compaction and strength gains result. Unfortunately, this sphere of influence depends on vibra tion strength, hopper geometry, hopper reinforcement details, solids flow properties, the level of solids in the bin, and how the solids were loaded. This makes vibrator selection and placement more of an art than a science and is, therefore, very error-prone. The frequent misapplication of vibrational activation begs the question, "Is there a better way?" The answer is yes.
Conserving Potential Energy
Passive activation occurs when properly shaped bins and hoppers conserve the potential energy of the con-tained bulk solid and gently concentrate this energy to break arches (obstructions on a bin's side walls), and if necessary, provide a first--in, first-out flow sequence from the bin.
The potential energy available from gravitational forces is simply the weight of the solids multiplied by the height of the bin through which it moves. This energy is dissipated by deforming the mass of solids (internal friction), and by frictional energy at the bin walls (surface friction.). When solids flow in bins and hoppers, there must be sufficient energy left to break cohesive forces that would otherwise cause hang-ups.
Vertical Bins Walls
Successful passive activation occurs when a hopper shape minimizes energy dissipation as the solid moves through the bin. Generally, this means reducing the internal deformation and energy lost to internal friction. The least energy dissipation occurs in a vertical wall bin with no convergence (see Fig. 2). In this case, the only energy dissipated inter-nally is that associated with changes in the solid's bulk density. Unfortunately, this bin design requires a very expen-sive, live-bottom, multiple-screw feeder equal to the bin's cross-section.
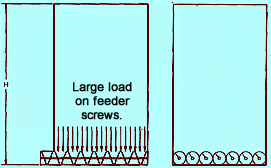
Figure 2: Minimum dissipation of potential energy
Feeders of this design require excessive power to dissipate the solid's potential energy during the feeding process. When such feeders are designed with an increased capacity in the direction of feed, arching and ratholing within the bin is virtually impossible; however, if even a short section of the screw's discharge end does not allow solids infeed, severe compaction occurs and arching is inevitable even with slightly cohesive solids.
Conical Hoppers
The most extreme case of internal energy dissipation occurs in a conical hop-per with flow at the walls (see Fig. 3). Conical hop-pers produce convergence in two directions simultan-eously and, as a result, maximize the internal energy losses. When a solid reaches the hopper outlet, there is lime energy left to break bridges and eliminate hang-ups.
Flow at the converging walls of a hopper will occur only if there is suf-ficient potential energy in a given volume of solids to satisfy both the internal energy dissipation and the wall friction energy dissipation. As a hopper's walls become flatter, the available potential energy for a given volume decreases until flow no longer occurs at the hopper's walls, but reverts to a smaller limited flow channel above the hopper outlet. This limited flow channel restricts energy dissipation to an almost vertical channel with Role converging, and reduces the stress level on the flowing solids. The functional energy loss from the flowing solids against the stationary solids dissipates -the remaining potential energy so that lime is left to break hang-ups at the hop-per outlet. As a result, hang-ups are more likely in a conical hopper without flow at the walls than in a conical hop-per with flow at the walls.
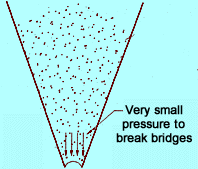
Fig. 3: Maximum dissipation of potential energy
The angle at which a solid converges on itself above a circular or square hop-per outlet is a function of the effective angle of internal friction. The smaller the internal friction angle, the larger the angle of convergence. For exam-ple, rock salt with a 60-degree effective angle of internal friction will have a convergence angle of about three degrees (measured from the vertical), whereas hard winter wheat, with a 25-degree effective angle of internal friction, may have a con-vergence angle of 30 degrees (measured from the vertical). The lower internal friction dissipates less friction energy both internally and at the surface between flowing and- non-flowing solids, which allows a larger flowing region.
For more information: Jerry Johansson, Jr., J.R. Johanson, Inc., 1237 Archer St., San Luis Obispo, CA 93401. Tel: 805-783-4484.
